オジサンです。
今回はコーヒーブレイクとして、婚活に一切関係ないネタを扱います。
ツイッターで出題させて頂いた問題の解答と解説を書きます。
(多くの方にご投票頂いて、ありがとうございました!)
出題した問題↓
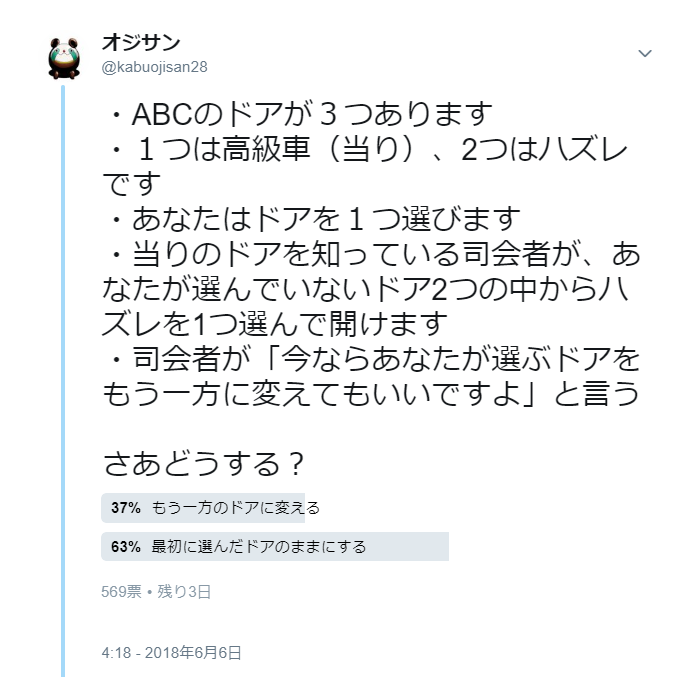
ご存知の方もいたようですが、これはモンティホール問題と呼ばれる確率論の問題です。
直感と実際にズレが生じる場合が多いことで有名です。
ブログ執筆時点で「最初に選んだドアのままにする」と回答した人が6割強を占めていますね~。
「最初に選んだドアのままにする」を選んだ人の理由は大体が以下の感じだと思います。
「ドアを変えても変えなくても確率は同じだから最初の直感を信じたい」
(もしドアを変えてハズレを引いてしまったら悔しい)
さらに、確率は同じと考えた人の中でも2つに分かれるのではないでしょうか
・そもそも3つの中に当りが1つだから、ドアを変えても変えなくても確率は3分の1
・司会者がハズレの扉を開けた時点で、どちらのドアを選んでも確率は2分の1
果たして、数学的には実際どうなのでしょうか・・・?
正解は、ドアを変えた方が当たる確率が高い。しかも2倍高い!
先に正解を言ってしまうと、司会者がハズレのドアを開けてからドアを変えた場合の勝率は3分の2、変えなかった場合の勝率は3分の1
実は、ドアを変えた方が2倍も当たりやすくなるんです!!
アンケートで「最初に選んだドアのままにする」と回答した6割強の人は損しますね~(^-^;
正解を聞いてもイマイチ納得できないのがこの問題の面白いところです。
次の章で何故そうなるか解説をしてみたいと思います。
確実に検証するために全通りのパターンをやってみる
確率の問題を解くときに最も確実な方法は可能な限り全通りのパターンを書き出してみることです。
今回の出題について実際にやってみましょう。
パターン数が多いのでまずは限定して書き出してみます。
まずは、あなたが最初にAのドアを選らんだ場合について考えます。
【ドアを変えない場合】
①当りがAの場合
最初にAを選ぶので、司会者はBかCのどちらかのドアを開けます。
あなたはドアを変えないので高級車をそのままGET(勝ち)
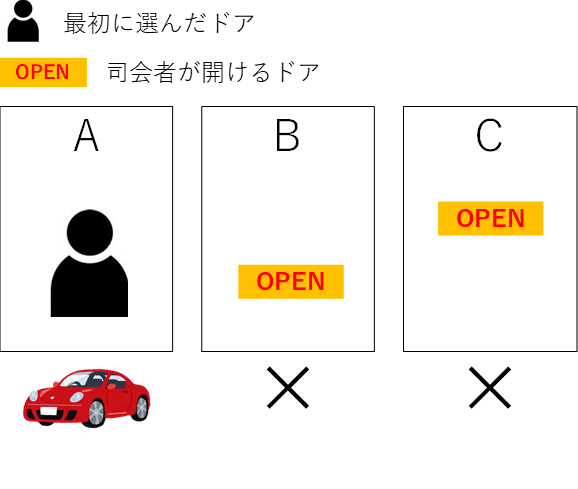
②当りがBの場合
最初にAを選ぶので、司会者は必ずCのドアを開けます。
(Bを開けたら車が出てきちゃいますから)
あなたはドアを変えないのでハズレになります(負け)

③当りがCの場合
同様の考えで、司会者は必ずBのドアを開けます。
あなたはドアを変えないのでハズレになります(負け)

つまり、ドアを変えない場合は1勝2敗になります。
では、続いてドアを変える場合について考えてみましょう。
【ドアを変える場合】
①当りがAの場合
最初にAを選ぶので、司会者はBかCのどちらかのドアを開けます。
あなたはドアを変えるので、司会者がBを開けた場合はC、Cを開けた場合はBに移動します。
いずれにせよ、あなたはハズレのドアを選ぶことになります(負け)
移動さえしなければ高級車をGETできたのに勿体ない!!

②当りがBの場合
最初にAを選ぶので、司会者は必ずCのドアを開けます。
(繰り返しますが、Bを開けたら車が出てきちゃいます)
あなたは最初に選んだAからBに移動するので高級車GET(勝ち)

③当りがCの場合
同様の考えで、司会者は必ずBのドアを開けます。
あなたは最初に選んだAからCに移動するので高級車GET(勝ち)

つまり、何とドアを変えた場合は2勝1敗となるのです。
ここまで、最初にAを選らんだ場合について解説しましたが、最初にBを選んでもCを選んでも全く同じことが起こります。(変えない場合は1勝2敗、変えた場合は2勝1敗)
まとめて図にすると以下のようになります。
【ドアを変えない場合】
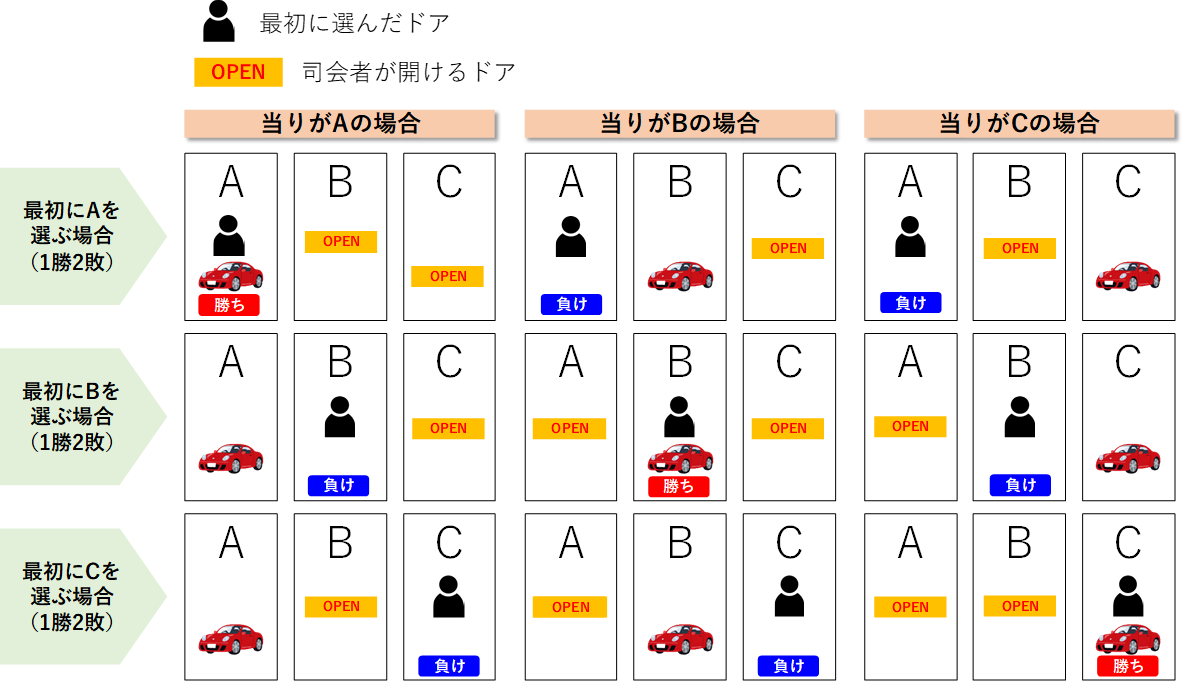
【ドアを変える場合】

やっぱりドアを変えた方が勝率は2倍高いですね。
ちなみに、このモンティホール問題はアメリカのテレビ番組(司会者はモンティさん)の余興だったらしいのですが、確率について数学者を巻き込んだ論争になったらしいですw
アンケートで「最初に選んだドアのままにする」を選んでしまった人も極めて正常な感覚だと思うのでご心配なく。
これからの人生で複数の中から1つの当りを選べという状況になった時、運営側に持ち掛けてモンティホール形式に誘導すると良いです。
(ただし、運営側が当りの場所を知っている必要がある)
うまく運営側が誘いに乗ってくれれば、確率を2倍にすることが出来ますよ♪
って、そんな場面あるんかいっ!
(ランキングサイトに参加しています。更新モチベが上がりますので宜しければクリックをお願いしますm(__)m)
オジサンはツイッターもやってますので宜しければフォローをお願いしますm(__)m









